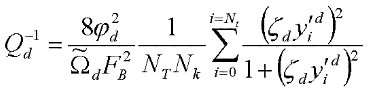Overview Simulations: Selective Kink Decoration Model Modeling Results Conclusion Interactive Geometric Kink Model Modeling Results Conclusion

© 2005 CSL

Equation of Motion of an Individual Kink in the Geometric Kink Chain

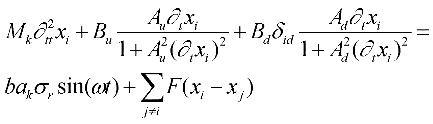
Coordinate Transformation: Global (x) to Local Coordinates (u)
Assumption: Nearest-Neighbor Interaction between the Kinks

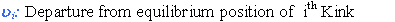
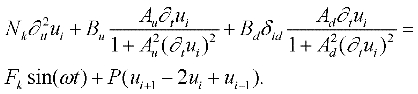
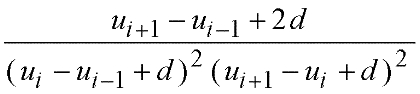
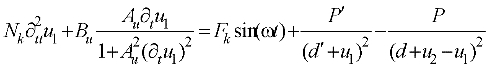
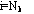
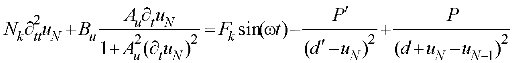
The time and space variables are normalized as;

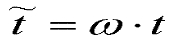
with respect to the driving frequency and;

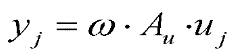
with respect to the distance travelled by a spread-out interstitial during one period of the motion.

Calculation of Dynamical Internal Friction Coefficient

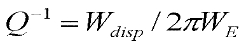
where

Wdisp: Energy Dissipated per cycle by the total kink population

WE: Maximum elastic energy stored in the kink chain during one cycle of external excitation

Dissipation energy;

Due to spread-out interstitials

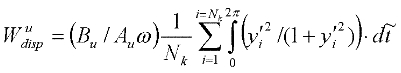
Due to decorator point defects

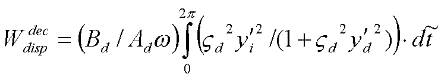
and,

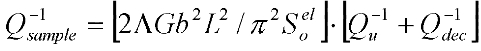
where 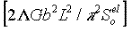is the macroscopic relaxation strength of the sample. This factor is previously described by Granato-Lucke, Schoeck, Seeger, and Ogurtani.

Finally the following equations were used to calculate the internal friction. For the Parent Damping Peak:

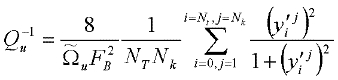
and

For the Decoration Damping Peak